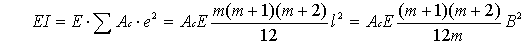PRIMARY DESIGN METHOD

A PRIMARY DESIGN METHOD ORIENTED TO THE DISPLACEMENT RESPONSE FOR HIGH-RISE REINFORCED CONCRETE FRAME BUILDINGS SUBJECTED TO EARTHQUAKES

ABSTRACT

This paper proposes a design method oriented to the displacement response for high-rise reinforced concrete frame buildings subjected to earthquakes. The shear stiffness distribution of high rise RC buildings was investigated considering bending and shear deformation. The required shear stiffness at the top of the building needs to be 0.3-0.5 times the stiffness at the base, so as not to produce whipping phenomenon. The outline of a design method is proposed based on these results and previous studies. The application of this method to 25 and 60 story buildings is shown. Drift responses during severe earthquakes were estimated and examined. The results satisfied the design criteria.

KEYWORDS

reinforced concrete structures; earthquake resistant design; displacement response; structural planning; deciding member section.

OBJECT

The author focused attention on the displacement response of reinforced concrete high rise building during an earthquake. Displacement response, estimation methods of response value, design base shear strength and distribution shape for design within acceptable damage without deformation concentration have been reported in previous papers (Shimazaki, 1988, 1992). These require that section dimensions be established at an early stage in structural planning. The structural designer usually establishes section setting from past design examples or previous design experience. At that time, if the behavior of the building during an earthquake can be determined by a simple technique, the design would be more effective.

For high rise buildings, if the stiffness distribution is unsuitable, whipping phenomenon can occur at the top, and the upper part will be subject to extreme shaking. On account of this, the section of the upper part is limited not from required strength considerations but by appropriate stiffness distribution. In the case of structural planning of a pure frame building, if the story and span numbers are fixed, column / beam sections of lower stories can be established by long term axial force limitation and base shear coefficient. Then the shear stiffness for lower stories is decided. After establishing a suitable shear stiffness distribution, dimensions of members can be decided.

This paper describes the examination of shear and bending deformation for reinforced concrete frame buildings, and the appropriate stiffness distribution to avoid whipping phenomenon. Finally, the method of deciding the member section is shown.

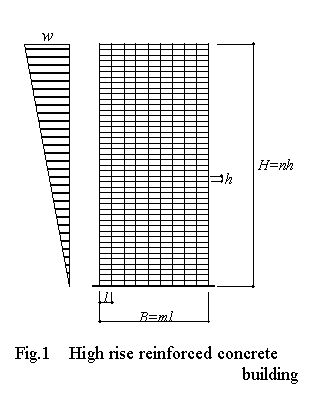
BENDING AND SHEAR DEFORMATION AND EIGEN MODES

Bending And Shear Stiffness

The bending stiffness EI of a frame building of height H and span m (building width B = ml) as shown in figure 1, is given by equation (1), in which the column section is square and section area is Ac.

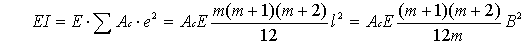････(1)

The story shear stiffness GA is given by equation (2) by the Muto's D method when the story height is h and stiffness coefficients obtained from stiffness ratio of columns to beams are all "a".

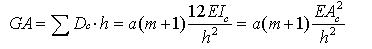････(2)

With a model of the bending-shear system fixed at base with height H

, constant bending stiffness EI and shear stiffness GA, the bending deformation and the shear deformation at the top are obtained by equation (3) where x is the distance from base.

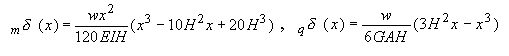････(3)

The deformation at the top (x = H) is given by equation (4).

････(4)

EI and GA obtained from equations (1) and (2) are substituted into this expression. When the stiffness ratio of column / beam is equal, the coefficient "a" becomes 0.5. Usually it comes within the range 0.2-0.4 because beam span is longer than height and the section of a column is greater than the section of a beam for a building designed by the beam yielding method. is known as the column ratio and it is about 0.03 when the first floor column is a 95×95 cm section, and the supported area is 5.5×5.5 m. The ratio of deformation of bending and shear deformation at the top is given by equation (5).

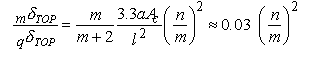････(5)

On the other hand, for the bending-shear model in which shear stiffness GA varies linearly to zero toward the top, it is given by the following equation.

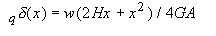････(6)

at the top,

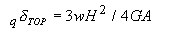････(7)

It becomes double that of the model with uniform shear stiffness. The ratio of bending and shear deformation is given by equation (8).

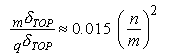････(8)

The ratio is between equation (5) and (8) for a real building, and would be 0.02(n/m)^2 . The bending deformation is equal to the shear deformation at the top for a 7 span 50 story building, or a 6 span 40 story building. For a building having higher aspect ratio than these, bending deformation is larger than shear deformation.

From equation (1), bending stiffness is proportional to column cross-sectional area, and shear stiffness is in proportional to the square of column cross-sectional area according to equation (2). Therefore, bending stiffness reduction is proportional to the square root of shear stiffness reduction by decreasing cross-sectional area of the column. The effect of stiffness distribution on eigen mode was examined using this relation in the study.

Eigen Mode In Uniform Stiffness Model

In the model used here, it is assumed that mass and story height over all stories are uniform, also that bending stiffness and shear stiffness are uniform. The ratio of bending deformation to shear deformation at the top was taken as a parameter, having the 5 values of 0.2, 0.5, 1.0, 2.0, and 3.0.

These eigen modes and story drift modes are shown in figure 2. For the first mode, the story drift is large at the lower part when the bending deformation rate is small, and is greatest at the top part when there is considerable bending deformation. The greater the rate of bending deformation, the larger the story drift in the higher part.

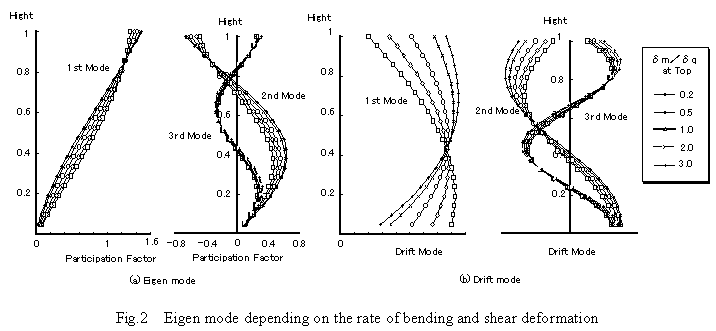
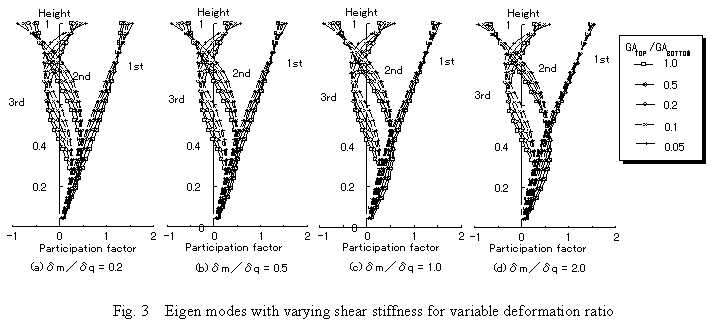
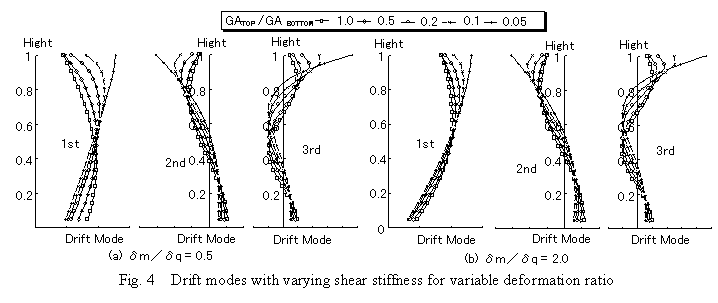
Eigen Mode In Decreasing Stiffness Model

Eigen mode when shear stiffness decreases linearly toward the top is examined here. Five values of shear stiffness reduction rate (Top stiffness/Bottom stiffness) were taken, 1.0, 0.5, 0.2, 0.1, and 0.05. They become 1.0, 0.71, 0.45, 0.32, and 0.22 as bending stiffness reduction rate. Eigen modes and story drift modes are shown in figures 3 and 4.

When there are few bending deformation, the change of eigen mode with stiffness reduction is considerable. The shape becomes susceptible to whip with stiffness reduction. The change in eigen mode with stiffness reduction with a large bending deformation rate is small. If shear stiffness at the top is more than 0.5 times that at the base and the bending deformation is smaller than the shear deformation at the top, the first mode shape of story drift never become large at the upper part. When the bending deformation is larger than the shear deformation at the top, the story drift is large in the upper part even for the uniform system. The tendency increases with decreasing the shear stiffness.

For the case where the shear stiffness decreases to 0.2 at the top, the story drift mode becomes considerable at the upper part, and will lead to whipping phenomenon by a combination with response spectrum. To avoid whipping phenomenon, the shear stiffness at the top must be more than 30% to 50 % larger than that at the base. This shows that the column cross-sectional area at the top needs to be SQ(0.5)≒0.7 times that at the top, and column dimensions needs to be SQ(0.7)≒0.85 times those at the base when the top shear stiffness is larger than 50% of the bottom stiffness.

METHOD OF DETERMING THE SECTION

Member Section Setting

The procedure for determining the section is setting the building scale, section dimensions, elastic model, and member strength. Finally, response values are estimated and the design criteria are confirmed. Because vertical load is proportional to the number of stories, the use of high strength concrete becomes necessary to achieve the allowable column section for high rise buildings.

In reinforced concrete column members, limit deformation and relation of axial force ratio are suggested from meaning of ductility considerations (Inai et al., 1997). The following equation is given for a column with constant axial force.

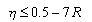････(9)

Here,η is the axial force ratio for core cross-sectional area and R is the drift limitation. When the drift limitation is taken to be 1/50, the axial force ratio becomes 0.36. Because core cross-sectional area is assumed to be 0.75 times that of the total section in the literature, it becomes around 0.27 at the axial force ratio limitation for total sections.

As the horizontal load is equivalent to weight of 4 story (Shimazaki et al., 1994), regardless of building height, column section is fixed only by the axial force limit for high rise buildings. Based on the assumption of a 0.25Fc axial force limit, 0.03 column rate and 1.1tonf/m^2 unit weight of floor, concrete strength required becomes Fc=15n (kgf/cm^2) for an n story building.

Section Setting Examples

As examples, the section dimensions and member strength will be determined for 25 and 60 story buildings. The buildings have a 5.8 m×6 m span, and a 3 m floor height, except for the first floor which is 3.5 m. Seismic load is given by the equation CB=0.24/T with eigen period T=0.02H (H : height of building) and 50cm/s the maximum velocity of the strongest design earthquake. Floor weight is assumed to be 1.0tonf/m^2 for seismic load and 1.1tonf/m^2 for column axial force. The materials used are SD590 (σy=6000kgf/cm^2) and Fc990 (σB=990kgf/cm^2) for the 60 story building, and SD390 (σy=4000kgf/cm^2) and Fc420 (σB=420kgf/cm^2) for the 25 story building.

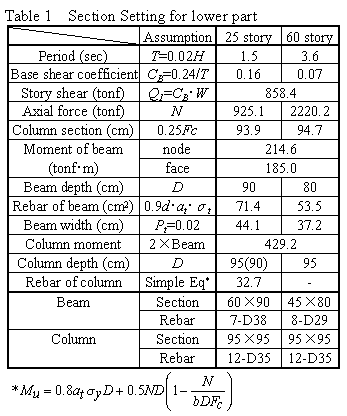
First, the sections of the lower story are set. Column sections are established from the long term axial force limit of 0.25Fc. Beam moment is calculated from base shear required, and section / reinforcing arrangement of the beam is established. Column strength at the base is made double the beam strength for yielding column at the base after beam yielding. If reinforcing bar can not be arranged in the column section, the section is changed. The calculation procedure and the section calculated are shown in table 1.

Next, section setting for each story is performed as follows:

Shear stiffness distribution is set with a linear distribution of 30-50 % at the top.
On the assumption that the stiffness coefficient "a" is constant, column section and beam section are decided and total bending stiffness and story shear stiffness are calculated from the set member section. If the assumed value of "a" is extremely different from that calculated, the section must be revised.
The drift for inverse triangle distribution horizontal load is calculated, and section revised if extremely uniform.
The eigen value problem is solved using the elastic stiffness calculated in 2). Using this result and design displacement response spectrum, the value of drift is estimated by SRSS (Square Root of Sum of Squares) of the 1st-5th mode drift. Here, the design displacement response spectrum is defined as pseudo-displacement response spectrum converted from the velocity response spectrum which is bilinear with maximum response velocity of 150cm/s. The design criteria are confirmed using this estimated value.
The required CB is determined from the first eigen period.
The required strength distribution and moment at nodal point are calculated using eigen mode and design response spectrum.
The beam moment at face position is calculated and necessary beam main reinforcement section is fixed.
The yield moment of beam at face is converted into nodal point moment, and nodal point moment divided by column's moment. The column shear force and story shear strength are determined, and confirmed to be approximately 1 to 1.2 times the required story strength.
With a moment strength magnification factor for the column of 1.5, the required column main reinforcement section is found.

Member section and reinforcing arrangement are shown in tables 2 and 3.

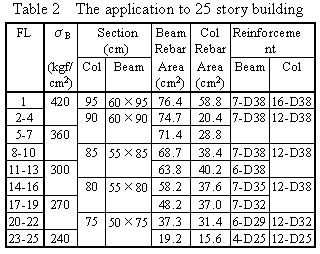
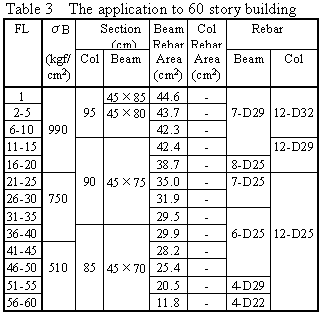
Comparison with the estimated reinforcing arrangement of the lower story shown in table 1, the reinforcing arrangement amount becomes large for the 25 story building, because the first period is short and weight increases. For the 60 story building, because the section is less than that of general structures due to the use of high strength materials, and the period is longer than the abbreviated expression, the required shear force becomes small, and the reinforcing arrangement also becomes small.

Estimation of Response Value

The maximum drift responses of the buildings estimated by the SRSS method for the standard ground motions with a maximum velocity of 50cm/s are shown in figure 5. The 1st-5th eigen modes by elastic stiffness and smoothed displacement response spectrum of 2 % damping were used. The maximum drift is almost less than the limit value of criteria (Story drift R=1/100 = 30mm).

INSPECTION BY FRAME ANALYSIS

Elastic Stiffness and Eigen Value

Frame response analysis is shown here using a one bay model. This model is used to consider the bending and shear deformation of column / beam member and shear deformation of the joint. Comparison of eigen period is shown in table 4, and comparison of eigen modes is shown in figure 6.

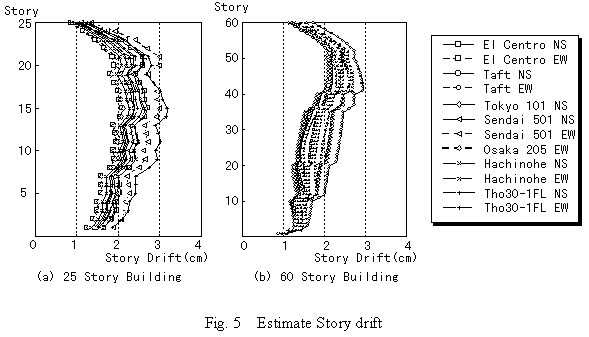
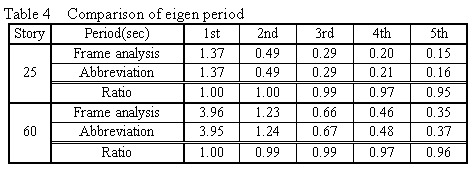
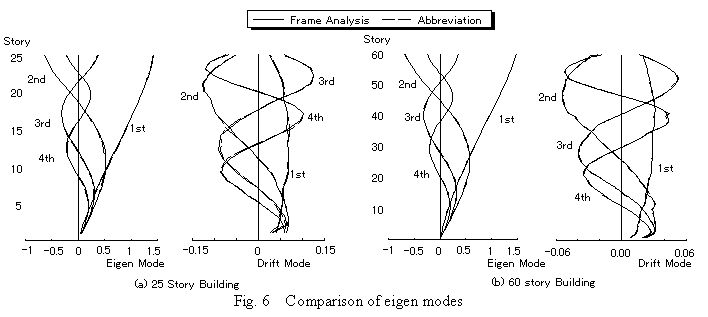
The eigen periods agree well. There is almost no difference in both total eigen mode and drift mode. It can therefore be said that the eigen period and eigen mode shape obtained by this abbreviated algorithm have sufficient precision.

Comparison of Response Value

Frame response analyses for the ground motion with a 50cm/s maximum velocity were carried out for 4 kinds of ground motion at El Centro NS, Taft EW, Hachinohe NS, and Tho30-1FL NS. The Giverson model was used as the member model. The damping was assumed to be 3% to the first eigen period and proportional for current tangent stiffness. The yield strength of the member was set up by the abbreviated expression shown in table 1. The Takeda model was used for nonlinear properties. For the beam, the first break point is 0.25 times the yield strength, and the stiffness reduction factor was assumed to be 0.20. For the column, the first break point was 0.40 times the yield strength, and the stiffness reduction factor was assumed to be 0.30.

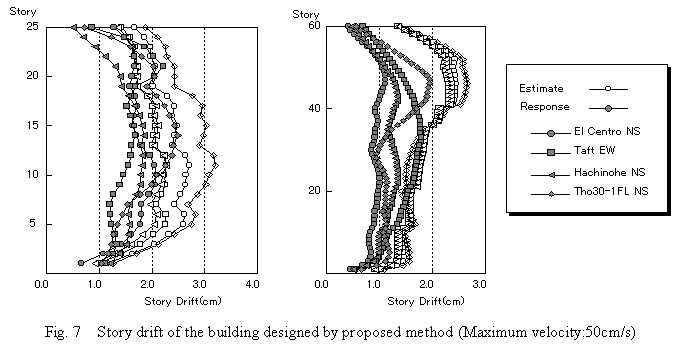
Calculated results are shown in figure 7. The response values by frame analysis are less than the estimated values and the distribution of drift for every ground motion is similar. Thus it can be said that if the section for a building is set by the proposed method, the building has the earthquake resistance intended by a design method such as drift limitation.

CONCLUSIONS

Shear stiffness at the top need to be 0.3-0.5 times the base stiffness so as not to produce whipping phenomenon.
Primary setting of the member can be achieve from base shear in the lower story, axial force limitation and stiffness distribution.
The building designed by the proposed method has the earthquake resistance intended by a design method such as drift limitation.

ACKNOWLEDGMENT

The author expresses his grateful appreciation to professor A. WADA of Tokyo Institute of Technology for his invaluable suggestions during this study.

REFERENCE

Shimazaki, K. (1988). Strong ground motion drift and base shear coefficient for R/C structures. Proc. 9th WCEE, V 165-170, Tokyo, Japan

Shimazaki, K. (1992). Seismic coefficient distribution of high-rise reinforced concrete buildings. Proc. 10th WCEE, 4281-4286, Madrid, Spain

Inai, E. and H. Hiraishi (1997). Structural design charts and equations of deformation capacity of reinforced concrete columns after flexural yielding. Proc. 11th WCEE (will be published), Mexico

Shimazaki, K. and A. Wada (1994). Design base shear coefficients for high-rise reinforced concrete buildings. Journal of structural and construction engineering, AIJ, No. 458, 99-108, Tokyo, Japan